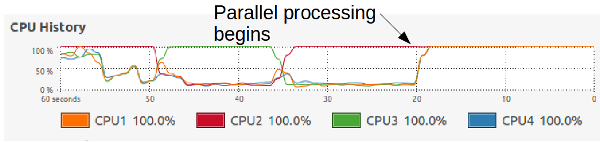
If you work with python and scientific instruments or other hardware with computer connections, I encourage you to add a driver for your instrument to the python library InstrumentKit. Although adding a device driver requires some effort upfront, I’ve found that it saves time in the long run. It resolves the pain of:
- needing a PDF or hard copy of the manual to look up features
- minimizing the amount of typing
- solving errors or eccentricities with your device now, once, instead of every time the device is used, or when you need to run an experiment on a deadline
- handling unit conversions correctly
- quickly transferring control code to a new computer
- helping your fellow scientists.
Now that I’ve (hopefully) convinced you that this is a good thing, I’ll go over adding an instrument to InstrumentKit. This tutorial is aimed at beginning python and git users, and will be aimed at creating an InstrumentKit driver for this lovely Thorlabs Piezo Controller:

Fork the InstrumentKit repository
Create a Github account, if you don’t already have one. Go to the InstrumentKit repository and click on the “Fork” button in the top right corner. If you have Windows, download Git for Windows. Open up git bash, go to a directory where you store your projects, and type:
git clone https://github.com/your_username/InstrumentKit
git checkout develop
git checkout -b thorlabs-mdt693B
To explain - first we created our own personal copy of the InstrumentKit repository (we forked it), then we made a copy on our computer (git clone), then checked out the development branch (checkout develop), and finally we made a branch off of the development branch (git checkout -b thorlabs-mdt693B).
The doc subdirectory in InstrumentKit contains instrument use examples; the instruments directory contains the source code. Within instruments, instruments are sorted into subdirectories by manufacturer. There are two additional folders - tests, which contains unit tests, which allow developers to check that changes to drivers do not change the operation of the device, and abstract_instruments, which contains generic code related to multiple devices. For example, for serial devices, it defines a generic SerialCommunicator device with query and command methods. Using an abstract instrument class allows you to avoid the most common ways that a serial communication protocol can be messed up.
Creating the Instrument
Create a new file under instruments->thorlabs called mdt693B.py.
InstrumentKit
└── instruments
└── thorlabs
├── __init__.py
├── lcc25.py
├── _packets.py
├── pm100usb.py
├── sc10.py
├── tc200.py
├── thorlabsapt.py
├── thorlabs_utils.py
└── mdt693B.py
In mdt693B.py, start off by adding the bash path to python, then a comment declaring what the module is for:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Provides the support for the Thorlabs MDT693B Piezo Controller.
Class originally contributed by Catherine Holloway.
"""
Next, like most python files, we need to import things. absolute_import and division are imported for python 2 to 3 compatibility. InstrumentKit uses the quantities library to handle unit conversion, but the convention is to import it as pq as most of the units are defined by single characters, so typing is minimal. For example, in this driver, we will be making use of pq.V. Our device is going to use the abstract_instrument Instrument as a template. We will also use the templates ProxyList, bool_property, int_property and unitful_property.
# IMPORTS #####################################################################
from __future__ import absolute_import
from __future__ import division
import quantities as pq
from instruments.abstract_instruments import Instrument
from instruments.util_fns import ProxyList, bool_property, int_property, \
unitful_property
# CLASSES #####################################################################
class MDT693B(Instrument):
"""
The MDT693B is is a controller for the voltage on precisely-controlled
actuators. This model has three output voltages, and is primarily used to
control stages in three dimensions.
The user manual can be found here:
https://www.thorlabs.com/drawings/f9c1d1abd428d849-AA2346ED-5056-1F02-43AE1247C3CAB43A/MDT694B-Manual.pdf
"""
The class keyword are like namespaces in Visual Basic or C#, or structs in C. This allows us to organize the attributes of devices in a logical way within a hierarchy. For example, we can imagine a multichannel voltage device being accessed like:
mc = MultichannelVoltageSupply()
mc.num_channels = 4
mc.channel[3].voltage = 3*pq.V
mc.channel[1].enable = True
the __init__ keyword is like a constructor on C++ classes - it gets called any time MDT693B() is called, and contains the code we want to run on initialization. Our device is based on the template Instrument, so in our intialization function, we need to call Super on it to make sure the Instrument gets initialized. Next, from the manual we can read that each query or command is terminated by a Carriage Return (\r) and Line Feed (\n) character, and that the device will print a prompt character when it is ready for new input. If we define these variables in our init, they will be passed up to Instrument when query or sendcmd are invoked, and will be handled appropriately. The variable self._channel_count is used to tell the ProxyList template that this device has three channels.
def __init__(self, filelike):
super(MDT693B, self).__init__(filelike)
self.terminator = "\r\n"
self.prompt = "> "
self._channel_count = 3
In python, all class methods take self as the first word. self is like the this keyword in C++ or Java. The second argument to the initialization is a pointer to the active serial communication channel - it is created and sent to the MDT693B using the Instrument.open_serial method.
We’ve created the skeleton of our driver, now we need to add it to the file instruments/thorlabs/__init__.py so that it can be found once InstrumentKit is installed:
from .mdt693B import MDT693B
Now, we’ll be able to access our device from any python script as:
from instruments.thorlabs import MDT593B
Using Factories
Now for the actual meat and potatoes of the driver. The commands are defined on page 18 of the User Manual.
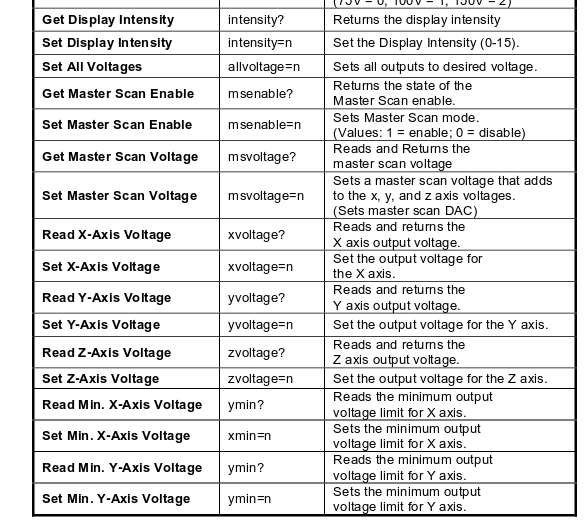
One thing to notice is that the commands for all three channels are relatively similar. We can minimize our typing by creating a generic channel class within our MDT693B class:
class Channel(object):
"""
Class representing a channel on the MDT693B
"""
__CHANNEL_NAMES = {
0: 'x',
1: 'y',
2: 'z'
}
def __init__(self, mdt, idx):
self._mdt = mdt
self._idx = idx
self._chan = self.__CHANNEL_NAMES[self._idx]
This initialization function is a bit more confusing - self._mdt is a link back up to the parent device, self._idx is the index value of the channel, and self._chan is a printable version of the channel name, which will be useful in generating the commands. From the manual, we can see that every channel has exactly three properties - the current set voltage, and the minimum and maximum allowable voltages. We would like to be able to set or get these variables as easily as you would any other independent variable, thus we should use the @property decorator. A getter/setter pair look like this:
@property
def voltage(self):
"""
Gets/Sets the channel voltage.
:param new_voltage: the new set voltage.
:type new_voltage: quantities.V
:return: The voltage of the channel.
:rtype: quantities.V
"""
return float(self._mdt.query(self._chan+"voltage?"))*pq.V
@voltage.setter
def voltage(self, new_voltage):
new_voltage = new_voltage.rescale('V').magnitude
self._mdt.sendcmd(self._chan+"voltage="+str(new_voltage))
This code may look confusing or pointless for those unfamiliar with object-oriented programming, but it will be invaluable once you’re used to it. It allows us to do things like:
print(mdt.channel[0].voltage.rescale('mV')
or
mdt.channel[0].voltage = my_joules/my_current
The first method of this pair, under the @property decorator, tells the parent device to send the query “xvoltage?” (if on channel 0, for example), convert the resulting string to a float, then assign its units as volts.
The second method of this pair, under the @voltage.setter decorator, re-scales the input value to volts, then sends the command “xvoltage=10” (if the new value was 10 V) to the device.
The same getter/setter pairs are copied for the minimum and maximum voltages.
In order to tell the MDT693B device that that channels 0-2 point to a voltage channels with the labels ‘x’, ‘y’ and ‘z’, we need to add a channel property that calls the ProxyList template:
@property
def channel(self):
"""
Gets a specific channel object. The desired channel is specified like
one would access a list.
:rtype: `MDT693B.Channel`
"""
return ProxyList(self, MDT693B.Channel, range(self._channel_count))
The rest of the properties defined in the manual follow a common pattern, so we can use existing templates (also sometimes called factories) in InstrumentKit to define them.
For example, enabling/disabling the master scan function is a prime target for a boolean property, since it has only two values:
master_scan_enable = bool_property(
"msenable",
"1",
"0",
doc="""
Gets/Sets the master scan enabled status.
Returns `True` if master scan is enabled, and `False` otherwise.
:rtype: `bool`
""",
set_fmt='{}={}'
)
Here, we use the first three values to declare the property keyword, then the values returned by the device for enabled and disabled. The set_fmt variable is used to define the format for the commands.
The display screen brightness is a unitless property, thus we can use the int_property to generate it:
intensity = int_property(
"intensity",
valid_set=range(0, 15),
set_fmt="{}={}",
doc="""
Gets/sets the screen brightness.
Value within [0, 15]
:return: the gain (in nnn)
:type: `int`
"""
)
The manual defines the valid range of values for intensity as being between 0-15. If it gets something outside of that range, it will likely behave oddly or report an error message, which will mess up serial communication. If we use this template, we can catch these out-of-bound errors before they get set to the device.
Finally, to show off another template, consider the master scan increment voltage. It is a unitful property - the value returned by the device is in volts, rather than the unitless integer setting for the screen brightness intensity. Here, a unitful_property template can be used:
master_scan_voltage = unitful_property(
"msvoltage",
units=pq.V,
set_fmt="{}={}",
doc="""
Gets/sets the master scan voltage increment.
:return: The master scan voltage increment
:units: Voltage
:type: `~quantities.V`
"""
)
It is the same as the two previous templates, except with the units variable set to volts to declare that the master_scan_voltage is in volts.
Creating an Example Script
Now that you’ve finished your driver, a sample script should be included so that others know how to use your device. Sample scripts are stored under doc/examples and then sorted by manufacturer:
InstrumentKit
└── doc
└── examples
└── thorlabs
└── ex_mdt693b.py
ex_mdt693b.py looks like this:
"""
An example script for interacting with the thorlabs MDT693B piezo driver.
"""
import quantities as pq
from instruments.thorlabs import MDT693B
mdt = MDT693B.open_serial(vid=1027, pid=24577, baud=115200)
for i in range(0, 3):
print("The voltage on ", i, " is ", mdt.channel[i].voltage)
print("The minimum on ", i, " is ", mdt.channel[i].minimum)
print("The maximum on ", i, " is ", mdt.channel[i].maximum)
mdt.master_scan_voltage = 1*pq.V
mdt.master_scan_enable = True
Although the method open_serial can be called by specifying a port, such as COM8 or /dev/ttyUSB0, it can also be specified using the device’s vid, pid, and optional serial number. As assigned ports can change hap-hazardly based on the order in which devices are plugged into the computer, or at the whims of the operating system, it is often preferable to open the serial connection with the vid/ pid pairs instead of the port. These IDs can be determined either by opening the port’s preferences under the device manager on Windows, or with the command lsusb in Linux.
If you have multiple devices with the same product and vendor ids, you can differentiate them by the optional variable serial_number, i.e.:
hardware1 = Device.open_serial(vid=1027, pid=24577, serial_number="aaaaaaaaa", baud=9600)
hardware2 = Device.open_serial(vid=1027, pid=24577, serial_number="aaaaaaaab", baud=9600)
The sample code opens a serial connection on this port and passes it to the MDT693B class for initialization. Then, it prints the voltage values for the three channels, then sets the master_scan_voltage and finally enables the master scan.
Contributing Back
Once your driver is finished, you should write unit tests for it, but that is enough material for another post. To contribute the device back to the community, stage your changes for a commit. In git bash, type the following:
cd InstrumentKit
git add instruments/thorlabs/__init__.py
git add instruments/thorlabs/mdt693b.py
git add doc/examples/thorlabs/ex_mdt693b.py
git commit -m "added MDT693B driver"
git push origin thorlabs-mdt693B
We changed directory into InstrumentKit, then added the three files we changed to the repository, then created a commit with the message added MDT693B driver, then pushed it to our github repository with the branch name thorlabs-mdt693B.
Once that is branch is public on github.com, we can create a pull request on github.com/Galvant/InstrumentKit. This allows the original developers of InstrumentKit to look over and approve our code. Hopefully the changes will be minimal, and your new driver will be available to others!